MONOPULSE TRACKING .. FEED ELEMENTS

Having seen the basic principle of Monopulse Tracking we now concentrate on the special components and circuits used for the derivation of actual tracking errors.

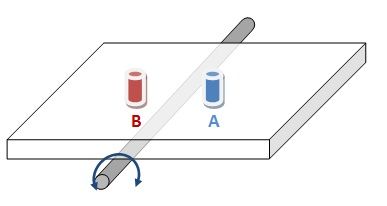
Antenna and Feed:

Recall the figure from last post reproduced on right.

A voltage proportional to the angular difference 

between Antenna axis and Target can be derived

by vectorial subtraction           ( A - B ).

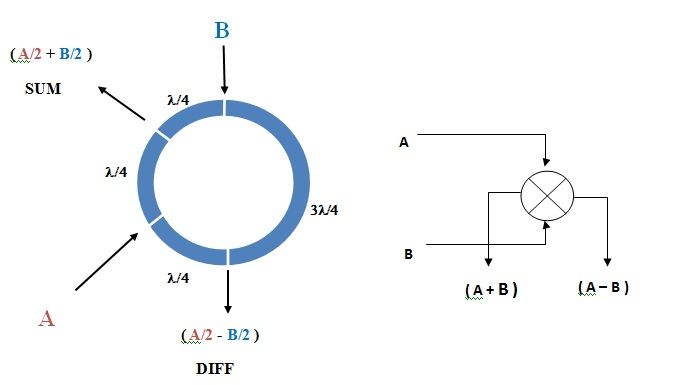
How do we derive the error signals from these  elements? We use what is called a Monopulse comparator. In one of the simplest forms  transmission lines of    l/4 and 3*l/4  are used in a ring fashions  as shown in next  figure.

The working principle is straight forward:

A  gets divided equally into two paths  each with a strength  A/2 ; 
One travelling to SUM port and 
another A/2 travelling to  DIFF ( = Difference )  port .

A similar split happens to B input.

At SUM port both A/2 and B/2 travel same path length and so they get added vectorially  to ( A/2 + B/2 ).

At the DIFF port A/2 components travels l/4   while the B/2 component travels  3l/4,  that is it travels l/4 +  2l/4 ( = l/2 )  and so the output becomes  A/2 plus (  B/2 with a phase reversal ),  so effectively you get ( A/2 - B/2 ) at the output. 

 

Althogh really the values are   ( A/2 + B/2 )    and   ( A/2 - B/2 )  they are denoted as ( A + B )    and   ( A  -  B )   which though theoretically wrong is the convention universally used for simplicity as we are not  doing a critical mathematical evaluation.

So we will use SUM = S =  ( A + B )    and  DIFF = D =  ( A  -  B ) as the convention  here onwards.

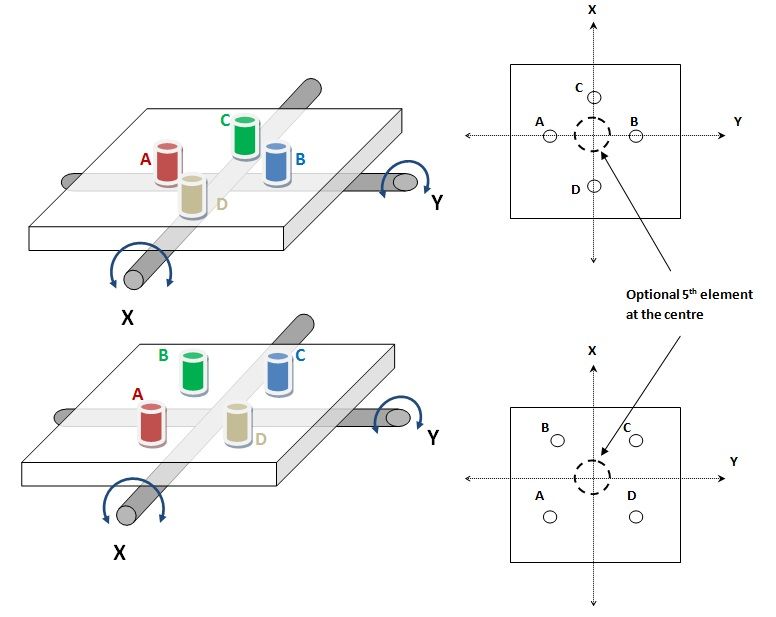
Two Axis Monopulse Feed:

We have seen that two elements are required to measure the angular difference for one axis.

 Antennae generally have two axes for Horizon to Horizon coverage hemisphere ( e.g.  AZ/EL   or  X/Y   or  Ha/Dec   etc. ).

It follows that there should be 4 elements to track in 2 axes.

In the example we assume that there are two axes X and Y supporting the antenna  and  the four elements can be placed in two fashions .. 

a.       Cross or On axis elements  arrangement  where the elements are mounted on axes  and

 the  error about X axis would be given by the quantity ( A – B )  
and Y Error would be ( C – D ).

While another arrangement would be

b.      Diagonal arrangement where the elements are placed in a 2 on each side of axes equally spaced from each axis and In this  case X arror would be (  ( A + B ) – ( C + D ) )   
      and Y Error would be ( ( A + D ) – ( B + C ) ) .

Two arrangements are graphically shown in the figure below.

Notice that in second case the error is a difference of two additions so  it is less prone to errors and is more sensitive.  That is the reason why it is commonly used.

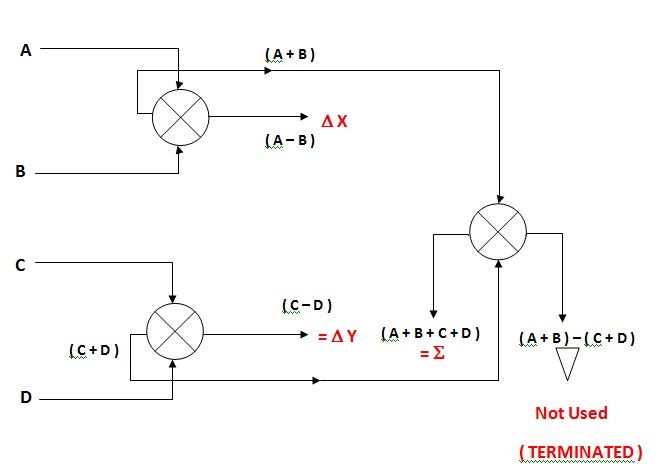
How do we derive the error signals from four elements?   We use a set of Monopulse comparators.

In  1^st case of Cross  arrangement of elements we use a set of 3 hybrids as shown hree.

Notice that we derive not only D X     and   D Y     signals but also  S   which can be  used as the input to communication data receiver.

Four hybrids are required to derive tracking errors if we use the 2^nd  i.e. Diagonal arrangement of elements as shown below.

Although 4 elements are sufficient to derive errors in two axes,  several other  more complex arrangements are used in sophisticated applications. 

One of the most common is to use a 5^th element at the centre of 4 elements A thru D as DATA pickoff element. This is useful in Parabolic reflector antennas since the error elements are always away from the prime focus of main reflector so receive less signal than what is available at the prime focus.   More on this subject in a later post.

We have shown here the most commonly used arrangements. The elements themselves could be Dipoles/Cross-Dipoles/Helices or Horns. There are several complex variations in use .

A few designs also use a single  Horn feed fabricated such that Error  outputs are derived at the output by multimode horn excitations .

There are also multielement feeds wherein  upto 12  elements are used to derive the Errors for better sensitivity and flatter phase response over wide frequency range of operation.

We will not go into more complex configurations but just mention here that in reflector antennas ( e.g Parabolic or Cassegrain ) generally a fifth element is added in the centre. This is not for tracking but is used as an independent DATA receiving element.

Next post covers the overall tracking system including error computing processor.

 Back to Main Index